Hallo,
ich möchte gerne die mathematischen Grundlagen vorstellen, die die gemessenen Rotationsgeschwindigkeiten beschreiben, die man misst, wenn man den Spektrographen-Spalt über eine rotierende Gasscheibe legt.
Das Modell ist dabei recht einfach - man geht von einer rotierenden Gasscheibe aus, die eine Keplersche Rotation aufweist:
=\sqrt {\frac{G*M}{r}})
Mit zunehmender Entfernung r vom Zentrum der Scheibe nimmt die Geschwindigkeit ab. Die Rotationsgeschwindigkeit ist ein Vektor, der tangential ausgerichtet ist, d.h. in der Scheibenebene liegt. Für die gemessene Rotationsgeschwindigkeit ist nun die Lage der Scheibenebene, relativ zur Beobachtungsrichtung, wichtig - diese bestimmt die radiale Komponente des Geschwindigkeitsvektors, und damit die messbare Rotationsgeschwindigkeit. In dem Modell wird die Orientierung Scheibenebene-Beobachter durch die Inklination i beschrieben. Ist die Inklination 0° blickt man frontal auf die Scheibenebene, bei i = 90°betrachtet man die Scheibe "edge on", und man misst die maximalen Radialkomponenten.
Für die weitere Betrachtung nutzt man zwei Koordinatensysteme - zum einen das in der gekippten Scheibenebene, und zum einen das in der Projektionsebene, die senkrecht zur Beobachtungsrichtung steht. Die kreisförmige Scheibe wird durch die Verkippung (Winkel i) zu einer Ellipse in der Projektionsebene. In der Projektionsebene nutzt man die Koordinaten X,Y zur Identifikation eines Punktes in der Ellipse.
} = R^2)
Nun kommt der Spalt zum Modell hinzu: Der Spalt liegt in der Projektionsebene und überstreicht die Ellipse. Die Lage des Spaltes wird mit zwei Parametern beschrieben - zum einen mit dem Versatz b der Spaltlinie vom Zentrum (es ist der Abstand des Fusspunktes vom Zentrum) und zum anderen mit dem Winkel
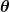
, der den Winkel zwischen Spaltlinie und der X-Achse bezeichnet. Die Spaltkoordinate wird mit s beschrieben und mit ihr durchläuft man bei der späteren Berechnung die gesamte Spaltlänge.
+s*cos(\theta))
+s*sin(\theta))
Für einen Punkt (X,Y) ergibt sich die radiale Geschwindigkeitskomponente
 * cos(\alpha)*sin(i))
. Der Winkel

liegt in der Scheibenebene und es besteht der Zusammenhang;
=\frac{Y}{X*cos(i)})
Mit diesen Modellannahmen kann man die durch den Spalt gemessene Geschwindigkeit wie folgt beschreiben:
*X}{(X^2+(\frac{Y^2}{cos(i)^2}))^\frac{3}{4}})
Die Geschwindigkeit des Systems, also bsp. die Fluchtgeschwindigkeit der Galaxie, in deren Zentrum die Gasscheibe liegt, ist

, der zweite Term liefert die Geschwindigkeitsbeiträge, die der Spalt "aus" der Projektionsellipse ausschneidet. Mit den Spaltparametern (b,
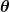
) kann man die Form der Geschwindigkeits-Modellkurve verändern. Die nachfolgende Grafik zeigt einen solchen Kurvenverlauf. Die X-Achse ist die Spaltkoordinate s, die Y-Achse zeigt die Radialgeschwindigkeiten - hier schon umgerechnet in Wellenlängen (Angstroem).

In dieser Grafik besitzt die Modellscheibe einen Durchmesser von 200 Pixeln und eine Verkippung von i=35°. Der Versatz zum Zentrum ist b = 20 Pixel und mit einem Winkel
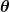
=5° liegt der Spalt fast parallel zur X-Achse. Das Resultat ist eine (fast) symmetrische Kurve der gemessenen Rotationsgeschwindigkeiten entlang des Spaltes. Das interessante bei dieser Modellbeschreibung ist der Umstand, das mit dem Versatz-Parameter b die Polstelle im Zentrum vermieden wird. Meist umgehen die Astronomen bei den galaktischen Rotationskurven dies, in dem sie den Zentrumsbereich ausklammern und dort eine starre Rotation ansetzen, die dann in eine Keplersche Scheibe übergeht.
Das Modell habe ich von F.Macchetto et al. übernommen, ihr findet den Fachartikel dazu unter ...
http://arxiv.org/abs/astro-ph/9706252. Dort gibt es auch weitere Bilder zur Erläuterung der Geometrie der Scheibenebene und der Projektionsebene.
Im folgenden werde ich dieses Modell benutzen, um damit die wellenförmige Variation der Ha-Linienlage zu beschreiben, die ich bei M82 gemessen habe. Im Prinzip lässt es sich das Modell aber bei allen System anwenden, in denen man eine Scheibe vermutet, die aus Gas besteht, das um ein massives Zentrum rotiert.
Schöne Grüsse,
Michael
_________________
___________________________________________
http://www.astro-images.de
14"-Hypergraph, Spektrographen: Dados & LISA