Dateianhang:
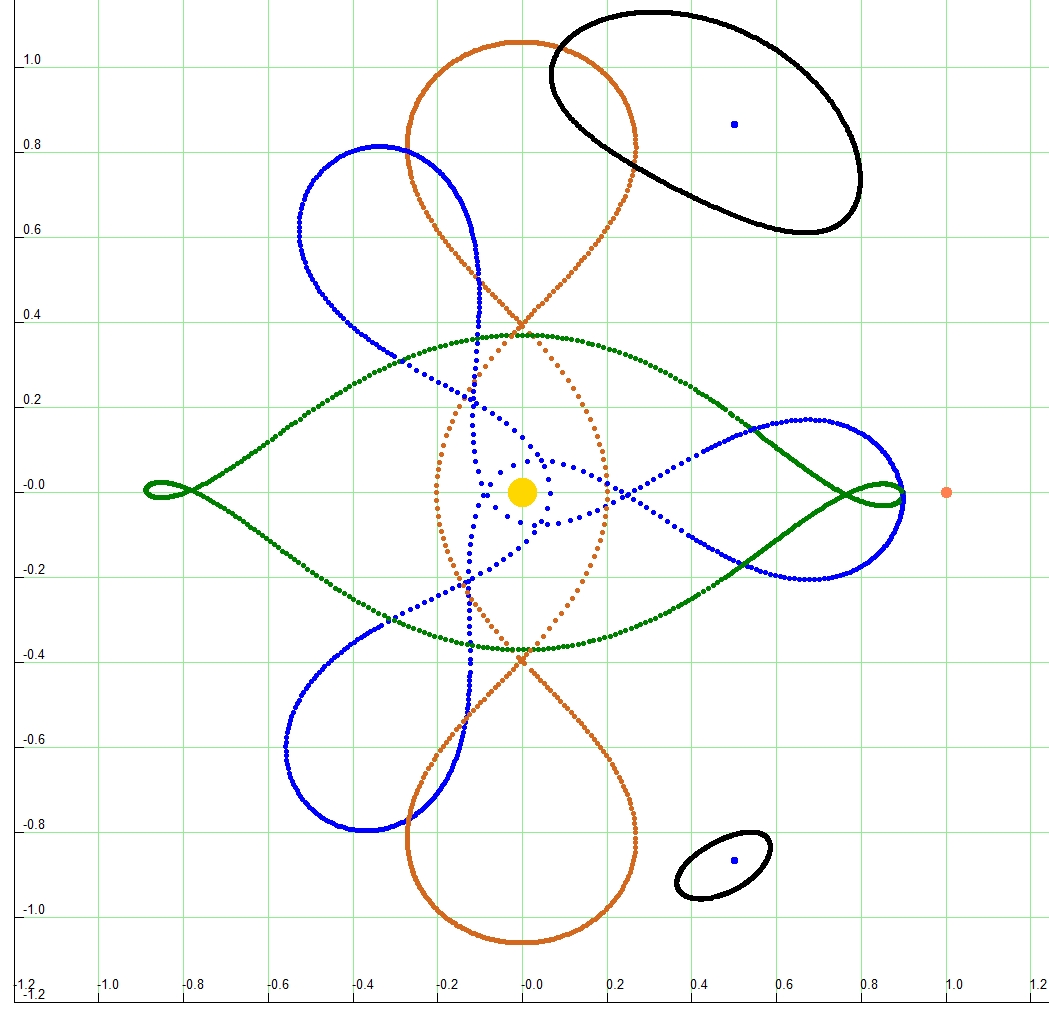Abb.jpg [ 251.54 KiB | 7948 mal betrachtet ]
Auf der Suche nach Lösungen der Bewegungsgleichungen für mehr als zwei Körper spielte das eingeschränkte Dreikörperproblem eine besondere Rolle. Zwei massebehafteten Körpern wird ein dritter, praktisch masseloser beigefügt.
Es gibt hierbei zyklische Bahnen im mitrotierenden Koordinatensystem. Diese lassen sich zwar nur numerisch berechnen, sind dann aber "für die Ewigkeit" gültig.
Ich fand es sehr interessant, damit zu experimentieren.
Anbei das Programm, was auch auf der
Internetseite der Fachgruppe liegt. Die
Grafikbibliothek muss wieder im selben Verzeichnis liegen.
Code:
# 3koerperPeriodisch.py - periodische Bahnen
from turtle import *
from random import *
from math import *
from plot import *
# globale Variable
G = 6.67408e-11 #Gravitationskonstante
mProAE = 149597870700 #Astronomische Einheit
sekProTag = 86400
true = 1
false = 0
# statische Variable für rkf5
rErrMin = 0
rErrMax = 0
dt = 0
N = 3 # Anzahl der Körper
r0 = [[0 for i in range(N)] for j in range(N)]
v0 = [[0 for i in range(N)] for j in range(N)]
a0 = [[0 for i in range(N)] for j in range(N)]
r1 = [[0 for i in range(N)] for j in range(N)]
v1 = [[0 for i in range(N)] for j in range(N)]
a1 = [[0 for i in range(N)] for j in range(N)]
r2 = [[0 for i in range(N)] for j in range(N)]
v2 = [[0 for i in range(N)] for j in range(N)]
a2 = [[0 for i in range(N)] for j in range(N)]
r3 = [[0 for i in range(N)] for j in range(N)]
v3 = [[0 for i in range(N)] for j in range(N)]
a3 = [[0 for i in range(N)] for j in range(N)]
r4 = [[0 for i in range(N)] for j in range(N)]
v4 = [[0 for i in range(N)] for j in range(N)]
a4 = [[0 for i in range(N)] for j in range(N)]
r5 = [[0 for i in range(N)] for j in range(N)]
v5 = [[0 for i in range(N)] for j in range(N)]
a5 = [[0 for i in range(N)] for j in range(N)]
# r0_4: Ergebnis für RKF 4. Ordnung zur Fehlerberechnung
r0_4 = [[0 for i in range(N)] for j in range(N)]
m = [0 for i in range(N)]
def startwerte():
# Orte und Geschwindigkeiten
r0[0][0] = -742448884.05
r0[0][1] = 0
r0[0][2] = 0
v0[0][0] = 0
v0[0][1] = -12.461410754
v0[0][2] = 0
r0[1][0] = 777607551115.94
r0[1][1] = 0
r0[1][2] = 0
v0[1][0] = 0
v0[1][1] = 13051.520863369
v0[1][2] = 0
r0[2][0] = 0 # wird vom Hauptprogramm gesetzt
r0[2][1] = 0
r0[2][2] = 0
v0[2][0] = 0
v0[2][1] = 0 # wird im Hauptprogramm gesetzt
v0[2][2] = 0
# Massen
m[0] = 1.988475415966536e+30
m[1] = 1.898568695e+27
m[2] = 0
def sq(x):
return x * x
def abstand(r, p, q):
return sqrt(sq(r[p][0] - r[q][0]) + sq(r[p][1] - r[q][1]) + sq(r[p][2] - r[q][2]))
def beschleunigung(N, m, r, a):
for p in range(N): # alle Beschleunigungen löschen
for k in range(3):
a[p][k] = 0
for p in range(N): # alle Planeten
for q in range(p + 1, N): # gegen alle anderen Planeten
R = abstand(r, p, q)
R3 = R * R * R
for k in range(3):
A = G * (r[q][k] - r[p][k]) / R3
a[p][k]+=m[q] * A
a[q][k]-=m[p] * A
def rkf5(tEnd, init):
global dt, rErrMin, rErrMax
t = 0
while(t < tEnd):
t = t + dt
beschleunigung(N, m, r0, a0)
for i in range(N):
for k in range(3):
r1[i][k] = r0[i][k] + 1 / 4 * dt * v0[i][k]
v1[i][k] = v0[i][k] + 1 / 4 * dt * a0[i][k]
beschleunigung(N, m, r1, a1)
for i in range(N):
for k in range(3):
r2[i][k] = r0[i][k] + 3 / 32 * dt * v0[i][k] + 9 / 32 * dt * v1[i][k]
v2[i][k] = v0[i][k] + 3 / 32 * dt * a0[i][k] + 9 / 32 * dt * a1[i][k]
beschleunigung(N, m, r2, a2)
for i in range(N):
for k in range(3):
r3[i][k] = r0[i][k] + 1932 / 2197 * dt * v0[i][k] + -7200 / 2197 * dt * v1[i][k] + \
7296 / 2197 * dt * v2[i][k]
v3[i][k] = v0[i][k] + 1932 / 2197 * dt * a0[i][k] + -7200 / 2197 * dt * a1[i][k] + \
7296 / 2197 * dt * a2[i][k]
beschleunigung(N, m, r3, a3)
for i in range(N):
for k in range(3):
r4[i][k] = r0[i][k] + 439 / 216 * dt * v0[i][k] - 8 * dt * v1[i][k] + 3680 / 513 * \
dt * v2[i][k] - 845 / 4104 * dt * v3[i][k]
v4[i][k] = v0[i][k] + 439 / 216 * dt * a0[i][k] - 8 * dt * a1[i][k] + 3680 / 513 * \
dt * a2[i][k] - 845 / 4104 * dt * a3[i][k]
beschleunigung(N, m, r4, a4)
for i in range(N):
for k in range(3):
r5[i][k] = r0[i][k] - 8 / 27 * dt * v0[i][k] + 2 * dt * v1[i][k] - 3544 / 2565 * \
dt * v2[i][k] + 1859 / 4104 * dt * v3[i][k] - 11 / 40 * dt * v4[i][k]
v5[i][k] = v0[i][k] - 8 / 27 * dt * a0[i][k] + 2 * dt * a1[i][k] - 3544 / 2565 * \
dt * a2[i][k] + 1859 / 4104 * dt * a3[i][k] - 11 / 40 * dt * a4[i][k]
beschleunigung(N, m, r5, a5)
for i in range(N):
for k in range(3):
r0_4[i][k] = r0[i][k]
# Ergebniss 4. Ordnung zur Fehlerberechnung
r0_4[i][k]+= dt * (25 / 216 * v0[i][k] + 0 * v1[i][k] + 1408 / 2565 * v2[i][k] + \
2197.0 / 4104 * v3[i][k] - 1 / 5 * v4[i][k] + 0 * v5[i][k])
# eigentliches Ergebnis 5. Ordnung
r0[i][k]+= dt * (16 / 135 * v0[i][k] + 0 * v1[i][k] + 6656 / 12825 * v2[i][k] + \
28561 / 56430 * v3[i][k] - 9 / 50 * v4[i][k] + 2 / 55 * v5[i][k])
v0[i][k]+= dt * (16 / 135 * a0[i][k] + 0 * a1[i][k] + 6656 / 12825 * a2[i][k] + \
28561 / 56430 * a3[i][k] - 9 / 50 * a4[i][k] + 2 / 55 * a5[i][k])
# Fehler ausrechnen. Benutzung erfordert eine while- statt einer for-Schleife
err = 0
for i in range(N): # welcher Körper gibt den größten Fehler?
localErr = 0
for k in range(3):
localErr+=sq(r0_4[i][k] - r0[i][k])
localErr = sqrt(localErr)
if (localErr > err):
err = localErr
if (init > 0): # Fehler wird in der ersten Runde so gesetzt,
rErrMin = err / 2 # wie es dem ersten dt entspricht
rErrMax = err
init = false
if (err < rErrMin): # Schrittweite verändern, falls der Fehler
dt*=1.2 # außerhalb der Grenzen
elif (err > rErrMax):
dt/=1.2
if (dt / sekProTag < 0.01):
Err = input("Schrittweitensteuerung versagt: dt erhöhen")
exit()
return t
# Hauptprogramm
startwerte()
rJ = r0[1][0] # der Jupiterradius ist konstant in dieser Rechnung
vJ = v0[1][1] # die Bahngeschwindigkeit auch
# Koordinatensystem einrichten
# x0 x1 xScale y0 y1 yScale
initKoor(-2.4,2.4,0.2, -2,2,0.2)
# alle im Text beschriebenen Beispiele
# X Y U V
# 0.2 0 0 2.89414 2:1
# 0.9 0 0 0.38 3:1
# 0.9 0 0 0.796 2:1
# 0.495 0.874685658 -0.8653265 0.4930764 1:1
# 0.495 0.874685658 -0.8653265 -0.4930764 1:1
# 0.45 0.953 -0.846264 0.428626 1:1
# 0.45 0.953 -0.846264 -0.428626 1:1
# 0.6 1.04 -0.72176 0.38641 1:1
# 0.6 1.04 -0.72176 0.38641 1:1
# die Ausgangswert in Jupitierradien und Jupitergeschwindigkeiten
X=0.45
Y=0.953
U=-0.846264
V=0.428626
T = 1 # simulierte Zeit in Jupiterumläufen (1)
P = 1000 # Anzahl Zwischenwerte (1000)
dt = 2.5 # 2,5 Tage
# Startwerte in die Felder einsetzen
r0[2][0] = X * rJ
v0[2][1] = V * v0[1][1]
r0[2][1] = Y * rJ
v0[2][0] = U * v0[1][1]
# den anderen Teil der Startwerte in SI umwandeln
dt = dt * sekProTag
UJup = 2 * pi * rJ / v0[1][1]
T = T * UJup
# Punkte für Jupiter und Sonne
Plot(r0[0][0] / rJ,r0[0][1] / rJ,20, "gold")
Plot(r0[1][0] / rJ,r0[1][1] / rJ,8,"coral")
Plot(0.5,sqrt(3)/2,5,"blue")
init = true
t = 0
while (t < T):
t = t + rkf5(T / P, init)
init = false # nur in der ersten Runde soll die interne Fehlergrenze gesetzt werden.
# in mitrotierene Koordinaten umrechnen (Skalarprodukt)
x = r0[2][0]
y = r0[2][1]
xJ = r0[1][0]
yJ = r0[1][1]
rP = sqrt(x * x + y * y)
xP = xJ * x + yJ * y
xP = xP / rJ / rJ
yP = -yJ * x + xJ * y
yP = yP / rJ / rJ
Plot(xP,yP,3,"black") # mitrotierende Koordinaten
#Plot(x/rJ,y/rJ,2,"black") # normale Koordinaten Asteroid
#Plot (xJ/rJ,yJ/rJ,2,"coral") # ... und Jupiter
update() # einkommentieren um den Bahnverlauf zu sehen
update()
done()
Registrieren
Anmelden
FAQ
Suche
